Terug naar Kakuro en probleemoplossen
Kakuro in het kort
Bij kakuropuzzels worden de getallen via redeneren & rekenen tevoorschijn getoverd. Daarbij wordt dat proces bewaakt door veldwachters, dat wil zeggen door somgetallen die rond het veld staan opgesteld. De puzzelregels zijn eenvoudig en lijken op de regels van Sudoku.
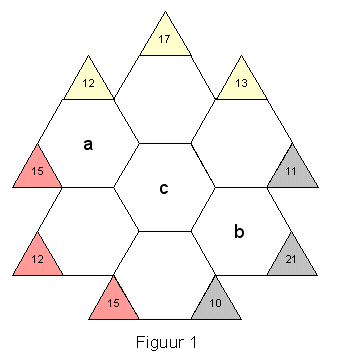
| Kakuroregels: 1) De veldwachters vormen de som van de bijbehorende rij tegelgetallen. Zo geldt bijvoorbeeld dat de tegelgetallen a, c en b samen 21 zijn. 2) Alleen de getallen 1 t/m 9 zijn toegestaan. 3) Getallen mogen in een rij maar één keer voorkomen. Figuur 2 |
Kakuropuzzels zijn er in allerlei vormen, van grillig tot regelmatig. De bloemkakuro van figuur 1 is een voorbeeld van de laatste soort en is zelfs draaisymmetrisch.
Op zich zijn deze bloemkakuro’s niet moeilijk om op te lossen. Neem bijvoorbeeld de bloemkakuro van figuur 1. Omdat 15 gesplitst kan worden in 9 en 6 of 8 en 7, zijn dat de vier mogelijkheden voor het getal a. Probeer er een en reken rond tot je eventueel vast loopt. Bij minder makkelijke kakuro’s is dat echter een tijdrovende en voor echte puzzelaars weinig inspirerende strategie. En bovendien weet je pas zeker of er maar één oplossing is als je alle mogelijkheden hebt doorgerekend.
De kunst is dus om zoveel mogelijk via redeneren het rekenpad te banen. Het is bijvoorbeeld meteen te zien dat invulling van 6 voor a niet mag vanwege het somgetal 12.
Bovendien zijn er bij symmetrische kakurovormen echte toverformules waarmee je bepaalde getallen tevoorschijn kunt toveren. Bij de bloemkakuro lukt dat bijvoorbeeld met het centrumgetal c.
Een toverformule bij de bloemkakuro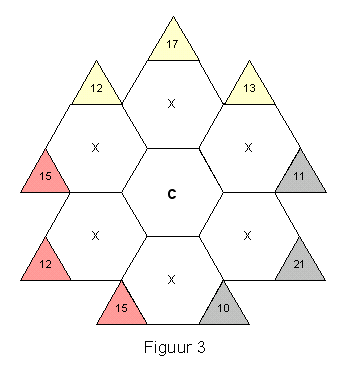
In figuur 3 kan het centrumgetal c tevoorschijn komen via het volgende ritueel 1:
1) Bepaal de som van de veldwachters die horen bij drie tegels: 17 + 21 + 12 = 50.
2) Bepaal de som van de kruisjesgetallen: 13 + 10 + 15 = 38 of 12 + 11 + 15 = 38.
3) Bepaal het verschil van de twee sommen: 50 – 38 = 12.
4) Deel het verschil door drie: 12 : 3 = 4
5) c = 4
Het ontraadselen van de puzzel is nu eenvoudiger geworden.
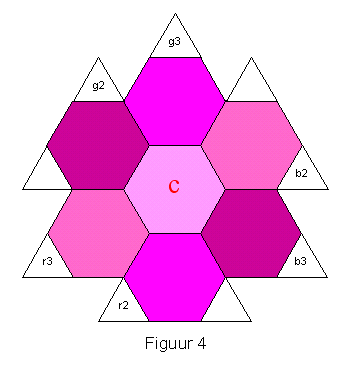
Voor de liefhebbers van echte formules zijn van figuur 3 zes getallen vervangen door symbolen (zie figuur 4). De volgende formule komt dan tevoorschijn:
C = { (g3 + r3 + b3) – (g2 + r2 + b2) } : 3
Een toverformule bij de driehoekkakuro
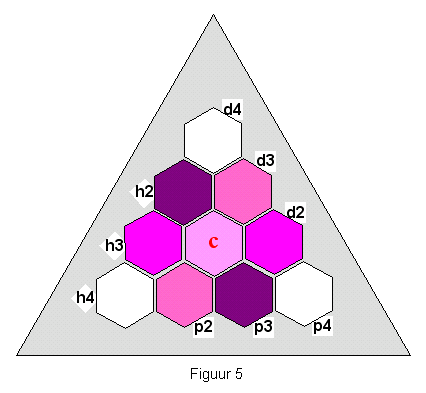
Het ritueel komt overeen met dat van figuur 4.
De pure formulevorm is vergelijkbaar met die van de bloemfiguur:
C = { (h3 + d3 + p3) – (h2 + d2 + p2) } : 3
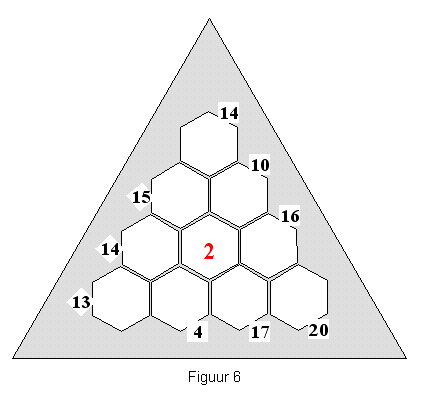
14 + 10 + 17 = 41.
15 + 16 + 4 = 35.
41 – 35 = 6.
6 : 3 = 2.
Waarmee het makkelijker is om de puzzel op te lossen.
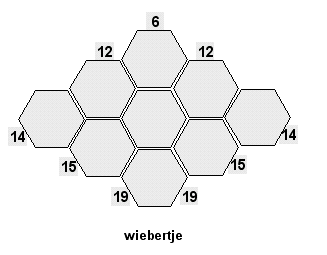
Het wiebertje hiernaast is een kakuro met een bijzondere vorm en met een bijzonder verhaal erachter. Zie voor dat verhaal Wingdingen en Wiebertjes (verslag) .
Ook bij deze vorm is de oplossing te vinden met oplostechnieken die standaard bij Kakuro horen. In Kakuro en probleemoplossen wordt daar dieper op ingegaan.
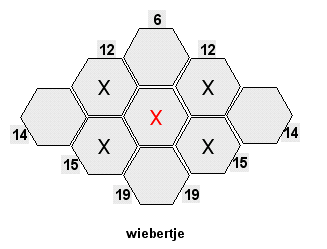
En ook hier zijn weer toverformules mogelijk, bijvoorbeeld om het centrumgetal te vinden. Deze keer kan de bloemvorm in de figuur niet benut worden maar zijn andere blikrichtingen nodig. Met behulp van de figuur hiernaast zal het niet moeilijk zijn na te gaan dat de volgende berekening een uitkomst heeft die gelijk is aan het centrumgetal.
{ (15 + 15) – (12 + 12) } : 2 = 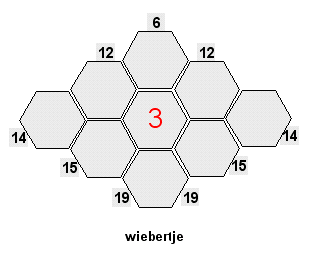
1 Er is een eenvoudiger ritueel mogelijk. Maar het ritueel dat gevolgd wordt, is ook van toepassing op andere symmetrische
kakurovormen zoals de driehoekkakuro die ook aan bod komt.