Terug naar Kakuro en probleemoplossen
H. den Hartog
Van oplossing tot oplossingsruimte
Puzzels die afkomstig zijn van puzzelsite’s en puzzelboekjes hebben bijna altijd één en niet meer dan één oplossing. Dat geldt ook voor Sudoku’s, Kakuro’s en andere logische ‘Japanse’ puzzels. Soms stuit men echter op puzzels waarbij het aantal oplossingen niet van te voren vaststaat en waarbij het zelfs mogelijk is dat de puzzel geen oplossing heeft. Wiskundig gezien wordt het dan pas echt interessant. Het denken verschuift dan van oplossing naar oplossingsruimte. Die ruimte kan geen, één of meerdere oplossingen bevatten. Zelfs ontelbaar veel is mogelijk. Genoeg speelruimte dus!
Bij logische puzzels kan men met redeneren greep krijgen op de oplossingsruimte. Dat is bijvoorbeeld handig als men zin heeft om een spelletje Fubuki online te spelen via http://jeuxflashfubuki.free.fr. Druk bij ‘Comment jouer?’ op het aandachtsbutton !!!! en het wordt duidelijk waarom dat zo is.
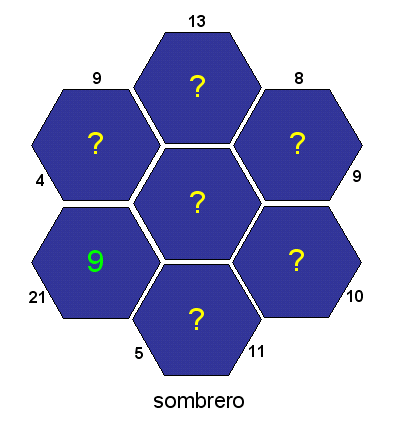
Ook bij de blauwe Sombrero van de spelsite van Toine van Broekhoven1 speelt het probleem van de oplossingsruimte. De blauwe Sombrero wordt besproken bij Kakuro (Speciale getallenvelden). In de figuur hiernaast is de sombrero weergegeven in aangepaste vorm.
De oplossing is niet moeilijk te vinden. Tenminste, als men afziet van de regel dat alleen de getallen 1 t/m 9 toegestaan zijn. Als men stap voor stap vanuit de groene negen aan het rekenen slaat, blijkt niet alleen dat het getal nul meedoet maar ook dat er, uitgaande van de negen slechts één oplossing is.
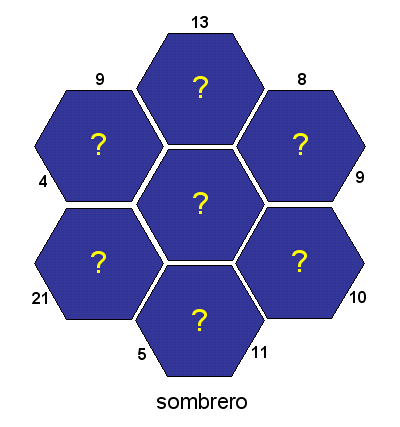Maar is dat ook zo als de groene 9 uit beeld verdwijnt? Dan gaat het om de situatie die hiernaast is afgebeeld. Is de oplossing met de groene 9 de enige? Is er misschien zelfs een oplossing te vinden die wel voldoet aan alle kakuroregels?
Dit puzzelspel met oplossingen levert op beide vragen het antwoord ‘nee’ op. En wil men de twee nee’s onderbouwen dan is het handig om er Toverformules bij kakuropuzzels bij te halen. Daarmee is te achterhalen dat het vraagteken in het centrum vervangen kan worden door het getal 7, onafhankelijk van wat er verder ook wordt ingevuld.
Het is niet moeilijk om met die 7 uit te vinden dat er nog een andere oplossing is met het getal nul. Ook blijkt dat zonder nul het oplossen strandt op de regel dat in een rij niet dezelfde getallen mogen voorkomen.
Spelen met oplossingen is een zinvol onderwerp voor de groepen 7 en 8 met het oog op de overgang naar de Wiskunde van het voortgezet onderwijs. Som-Som puzzels bieden daarvoor geschikt materiaal.
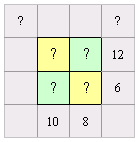
De figuur hiernaast met de vraagtekens behoort tot de categorie som-som puzzels. In de gekleurde vakjes horen getallen thuis die horizontaal en verticaal opgeteld de uitkomsten opleveren die in de grijze rand staan. De vraagtekens in de grijze rand vormen de diagonaal-sommen die horen bij de groene respectievelijk gele vakjes. Alle getallen zijn in principe toegestaan. In een rij mogen dezelfde getallen voorkomen. Kakuroregels gelden alleen als men daarvoor kiest.
|
Hoeveel oplossingen zijn er bij de som-som puzzel mogelijk uitgaande van de verzameling van de Natuurlijke Getallen (1, 2, 3, enz.)? Is er een oplossing mogelijk waarbij de diagonaalsommen aan elkaar gelijk zijn? Zo ja, wat is de oplossing? |
Het is niet moeilijk om een oplossing te vinden. ‘Gewoon’ wat invullen en rekenen leidt al tot succes. Tijd dus om wat te spelen met oplossingen. Dat kan aan de hand van de vragen hiernaast. Uitwerkingen treft men aan via Eerst zelf proberen! .
1 Anno 2007 was de spelsite via http://edusoft.town.nl direct te bereiken. Nu, anno 2013 is de software nog te achterhalen
via Oefensite JL Groep Tilburg.