Terug naar Kakuro en probleemoplossen

Bij het oplossen van een kakuro vormt splitsing van somgetallen meestal het begin van het oplosproces. Soms is het zinvol om het splitsen (even) achterwege te laten en te proberen om louter en alleen met somgetallen, een stap verder te komen. Dat wordt toegelicht aan de hand van de kakuro van afbeelding 1, waarvan in afbeelding 2 het kopstuk vergroot is weergegeven. Dat kopstuk bevat 19 cellen waarin getallen tevoorschijn moeten komen.
Afbeelding 1
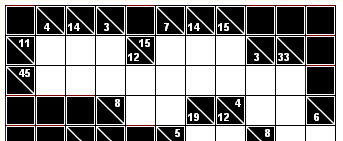
De som van de 19 te ontdekken kopgetallen is te bepalen door de somgetallen van de horizontale rijen bij elkaar op te tellen. Het resultaat daarvan is 83. Ook voor de verticale rijen, op één na, kan dat gedaan worden. De spelbederver is de 33-rij rechts want die loopt door. Het resultaat is 72. De twee kopgetallen van de 33-rij zijn dus samen gelijk aan 11.
Afbeelding 2
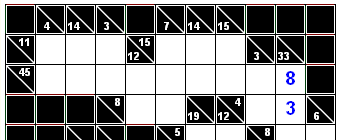
Daarmee blijkt de spelbederver te hebben gezorgd voor een onverwachte opening. Het is namelijk niet moeilijk om in te zien dat 11 zich splitst in de termen 3 en 8.
Afbeelding 3
Manipuleren met somgetallen bij de soort waartoe het Wingding behoort
Bij de standaardkakuro is manipuleren met somgetallen lang niet altijd mogelijk en meestal tamelijk omslachtig. Bij symmetrische kakuro’s met een zeshoekige celstructuur, zoals Wingdingen en Wiebertjes, biedt de manipulatiestrategie echter mogelijkheden die niet alleen wiskundig gezien interessant zijn maar ook een krachtige ondersteuning vormen voor het oplosproces. Dat wordt toegelicht aan de hand van het wingding van afbeelding 4 en de bloemkakuro van afbeelding 5.
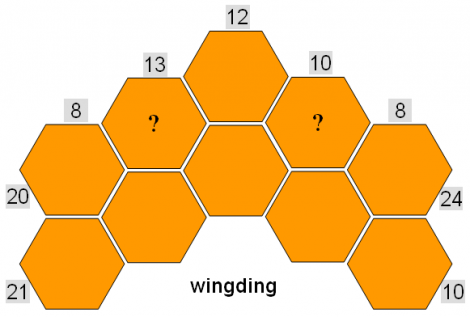 Bij het wingding kan het rechter vraagteken berekend worden op de volgende manier: (20 + 21) – (8 + 13 + 12) = 8.
Bij het wingding kan het rechter vraagteken berekend worden op de volgende manier: (20 + 21) – (8 + 13 + 12) = 8.
De lezer wordt uitgenodigd om deze ‘formule’ visueel te controleren in afbeelding 4 en zal daarna aanvoelen dat het formulekarakter slechts afhangt van de wingvorm. Vanwege de symmetrie van de figuur, kan een vergelijkbare ‘formule’ afgeleid worden voor het vraagteken links. In dit soort wingdingen kunnen dus al twee getallen bepaald worden (plus de twee eronder!), voordat overgegaan wordt op het normale reken- en redeneerwerk. Afbeelding 4
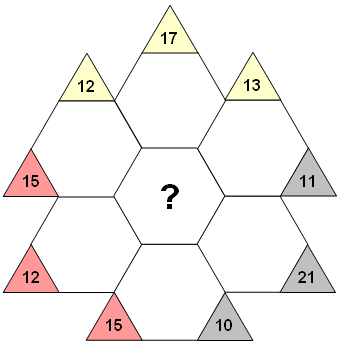 Bij de bloemkakuro gaat het om het getal in het hart van de bloem. Een mogelijke ‘formule’ daarvoor is:
Bij de bloemkakuro gaat het om het getal in het hart van de bloem. Een mogelijke ‘formule’ daarvoor is:
(12 + 17 + 13) – (10 + 15 + 13) = 4 of verkort:
(12 + 17) – (10 + 15) = 4. Ook nu wordt de lezer uitgenodigd tot visuele inspectie.
Bij dit soort puzzels is formule-denken binnen bereik van veel leerlingen en andere puzzelliefhebbers. Hopelijk zal dat hun plezier in dit aspect van wiskunde vergroten en hun onderzoekende puzzelhouding op een hoger niveau brengen.
Voor meer toverformules bij kakuro kunnen liefhebbers terecht bij Toverformules bij kakuropuzzels. Afbeelding 5